What are trusses and types of Trusses, frames

TRUSSES or FRAMES:

            Hello mechons, in this post we are going to explain to you about a little topic of the Engineering mechanics called Frames also called as Trusses. 

Before going to learn about the types of frames and its uses first we need to know about, 

{tocify} $title={Contents}

What are Trusses or Frames? 

A structure with several bars riveted or welded together are called Trusses or Frames. They basically provide strength and support to a construction.

To find the support reactions at the end, same principles as in beams are used, 

• Analytical method 
• Graphical method.

Types of frames 

End supports of frames are differentiated as,

1. Frames with simply supported ends.  
2. Frames with one free end and one hinged end. 
3. Frames with both end fixed.

Frames with simply supported ends:

           In this case, it is same as simple support beam. Here, two simple supports are used at the ends. So, two vertical forces are considered at the two ends of the frame.

(Example for simple supported frame) 

Free body diagram of Simple supported frame

(Free body diagram of simple supportrd frame) 

Problem:

Example problem for Frames with simply Supported ends (Fig 1.1)

(Fig-1.1)

→ A truss of 12 m span is loaded as shown in 

(Fig 1.1)

Given data:

Span AB = 12m

Let Ra be reaction at A

Rb be reaction at B

Now, equating Clockwise and Anticlockwise moments about the point A. 

(Rb×12) = (2×3) + (3×6) + (2×9) + (2×4)+(6×8)

Rb × 12 = 98 K-Nm

Rb = 98 K-Nm /12m

Rb = 8.167 KN

Ra = ( 2+3+2+2+6) - 8.167

Ra = 6.833 KN

Frames with one end hinged (pin jointed) and other end freely supported on rollers

(Free body diagram)

 

When a frame carries horizontal or inclined load, a pin joint and a free end is needed to compensate the load. Types of load applied on frames with hinged and roller end, 

• Horizontal loading 
• Inclined loading 

Problem

Example problem for frmae with one end hinged support and other end freely supported on rollers with horizontal loading (Fig 1.2)

(Fig 1.2)

Given data:

Span = 8m 

Let Ra be Reaction at A and Re be Reaction at E

Solution :

As one end is supported as roller the reaction will be at vertical whereas  At  "A" it will be both horizontal and vertical. 

Taking Moment about A, 

- Re × 8 = (2W × 2) + (W×2)

= 6W 

➝ Re = 6W/8 

Re = 0.75 W 

Vertical Component of  Reaction Ra 

Va = 2W - 0.75 W 

Va = 1.25 W 

Horizontal Component of Reaction Ra 

Ha = W (←) 

Reaction at A, 

Ra = {w2 +(1.25)2}1/2

Ra = 1.6 W

tan ं = W/ 1.25 W

tanं = 0.8

ं = 38.6 °

Frames with Horizontal Loading:

(Frames with horizontal loading) 

Resultant reaction's inclination with vertical is given by,

                       tan 𝚹 = ∑H / ∑V
            Here, ∑H = Algebric sum of Horizontal reactions,
                      ∑V = Algebric sum of vertical reactions.

 

Problem:

Example problem for frames with One end hinged and other end with roller support and horizontal load (fig 1.3).

(Fig 1.3)

Given data :

Span = 8m 

Let Ra be Reaction at A and Re be Raction be Reaction at E. 

Solution:

Taking moment about A, 

Re × 8 = (2W × 2) + (W×2)

  Re ×8 = 6W 

➝ Re = 6W/8 

Re = 0.75 W 

Vertical Component of  Reaction Ra 

Va = 2W - 0.75 W 

Va = 1.25 W 

Horizontal Component of Reaction Ra 

Ha = W (←) 

Reaction at A, 

Ra = {w2 +(1.25)2}1/2

Ra = 1.6 W

tan ं = W/ 1.25 W

tanं = 0.8

ं = 38.6 ° 

Frames with Inclined Loading:

(Free body diagram) 

The support reactions are found by two methods:
                      1. Analytical method
                      2. Graphical method

Problem

Example problem for frames with one end hinged and other end with roller support and with inclined loads (Fig 1.4).

(Fig 1.4)

Given data:

Span = 10m

Let Ra be Reaction at A and Rb be reaction at B. 

Solution:

1) Analytical method:

Perpendicular between support A and line of action of load at D. 

 5/ cos 30° = 5/ 0.866 = 5.8m 

Perpendicular distance between support A and line of Action of load at C

= 5.8/2 = 2.9m 

Equating clockwise moments and anticlockwise moments about A, 

Rb x 10 = 2 x 2.9) + (1 x 5.8) 

Rb x 10 = 11.6 

Rb = 1.16 KN

Total wind load = 1+2+1 = 4KN

Horizontal component of wind load load =  4Cos60° = 4 x 0.5

= 2KN

 Vertical component of Wind load 

= 4Sin60° = 4x 0.866 

= 3.464 KN

Balancing Vertical reaction at A=3.464-1.16 

= 2.304 KN

Ra = (2^2 + 2.304 ^2)1/2

= 3.05 KN

tan ं = 2.0/2.304

tanं = 0.868 

ं=41°

2) Graphical method:

(Graphical method) 

1. First draw the free body diagram and name the forces and reactions according to BOCO's notations. 
2. Add the forces together and assume them to act together at C.G (CENTRE OF GRAVITY) at C. 
3. Draw the line of action of resultant force to meet at line of action of roller support. 
4. Join OA, from O cut off OM equal to toatal componded load (i.e.  4KN) along the line of action of resultant force. 
5. Complete parallelogram OLMN, with OM as diagonal. 
6. Measure ON and OL. The length OL gives the magnitude and direction of Reaction Ra and also Reaction Rb magnitude. 
7. By measuring, we get 

Ra = 3KN

Rb = 1.2 KN

ं = 41°

Frames with Both End Fixed

The assumptions are, 

1. Reactions are parallel to direction of loads.

2. In case of Inclined loads, Horizontal thrust is equally shared between reactions. 

Problem:

Example Problem for Frames with both ends fixed (Fig 1.5).

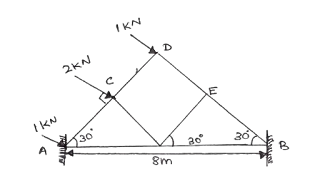(Fig 1.5)

Given data :

Span = 8m

Let Ra be Reaction at A and Rb be Reaction at B. 

Solution

Assumption 1:

Reactions are parallel to the direction of loads 

Equating moments at A, 

Rb x 8sin60°= (2x2/Cos30°) + (1x4/Cos30°)

Rb x 8 x 0.866 = 9. 24 

Rb = 9.24 / (8x0.866)

Rb = 1.33KN

Ra =(1+2+1) - 1.33

Ra = 2.67KN

Assumption 2 :

Horizontal thrust is equally shared by reactions. 

Total horizontal component of load, 

EH = 1cos60° + 2cos60° + 1cos60°

EH = 2KN

Horizontal thrust on each support, 

Rah = Rbh = 2/2 KN = 1KN

Now, Equating clockwise and anticlockwise moments about A, 

RBV x 8 = (2x2/cos30°) + (1x4/cos30°) 

= 8/0.866

RBV = 9.24 /8

RBV = 1.15 KN

RAV = [ 1sin60° + 2sin60° + 1sin60°] - 1.15 KN

RAV = 2.31 KN

Ra = {(1)^2 + (2.31)^2}^1/2

Ra = 2.52KN

tan ंa = 2.31/ 1 =2.31

ं a = 66.6° 

Similarly, Rb = ((1)^2 + (1.15)^2)^1/2

tan ं b =1.15/1 = 1.15

ं b =49°

Conclusion

That's all about the frames or trusses types, forumulae, and example problems in frames for now. I hope that you understand the definitions, formulae and types. 

If you have any queries or doubts regarding this topic don't hesitate put that in the below-mentioned comments section. We are here for you we will reply as fast as possible. 

And one more thing Always remember to 

Spark your brain and Throttle your knowledge!.